Prior remplace Diodore
2025-04-26, updated 2025-04-26 next - previous
Cet article avait été accepté pour paraître dans un numéro spécial de Philosophia Scientiae, mais au dernier moment, le rédacteur en chef de cette revue a décidé de le rejeter.
Le lecteur peut télécharger ici l’épreuve finale de l’article rejeté; le texte de ce blog éclairera peut-être ce qui a été précédemment jugé comme obscur ou comme faux, mais que je continue de penser comme correct et que je me suis efforcé de prouver.
1. Symbolisme
L’ensemble des symboles du langage-objet utilisé pour les démonstrations formelles de cet article est composé de deux sous-ensembles de symboles, dont le premier est celui des symboles du langage de la logique modale propositionnelle où \[ \lnot, \land, \lor, \to, \bot, Q, \Diamond, \Box, ),( \] sont respectivement les connecteurs usuels (négation, conjonction, disjonction et conditionnel), la constante du faux, la variable propositionnelle Q, les opérateurs modaux de possibilité et de nécessité, et enfin les parenthèses. Le second sous-ensemble contient deux symboles spécifiques à la logique temporelle minimale \(\mathbf{Kt}\) [1, pp. 13–70], c’est à dire les opérateurs temporels \(\mathbf{P}\) et \(\mathbf{F}\). La signification des opérateurs \(\mathbf{P}\) et \(\mathbf{F}\) est donnée par leurs règles d’introduction respectives dans le système de déduction naturelle étiquettée développé par Volpe [2] pour la logique temporelle, où a et b sont des repères temporels:
| \begin{prooftree}\AxiomC{$a: Q$}\AxiomC{$a < b$}\RightLabel{\(\scriptsize{~\mathbf{P}~I}\)} \BinaryInfC{\(b: \mathbf{P}Q\)} \end{prooftree} | \begin{prooftree}\AxiomC{$b: Q$}\AxiomC{$a < b$}\RightLabel{\(\scriptsize{~\mathbf{F}~I}\)} \BinaryInfC{\(a: \mathbf{F}Q\)} \end{prooftree} |
Les symboles qui appartiennent au métalangage dans cet article sont ceux de la dérivabilité syntaxique, de la relation d’ordre strict, des repères temporels indiqués par des lettres minuscules et un symbole de constante pour désigner un modèle:
\[\vdash, <, a, b, n, t, \mathcal{M}\]
2. Formalisation de l’argument de Diodore-Prior-Fitting
J’appelle “argument Diodore-Prior-Fitting” ou, plus simplement, “argument DPF”, l’argument de Diodore selon Prior [3], [4, pp. 32–33], dans la version semi-formelle de Fitting [5, pp. 38–40], sur laquelle la preuve de cette section s’appuie, sans faire usage cependant de la règle du modus tollens. Cette preuve sera développée dans deux styles de déduction naturelle: le style «arbre» de Gentzen, tel qu’il est utilisé par exemple par Negri et von Plato [6], et le style “drapeau” de Fitch, dans la notation de Magnus et al. [7], où les prémisses (notées PR) sont clairement distinguées des hypothèses (notées AS), celles-ci étant déchargées, contrairement à celles-là.
L’argument de Diodore (appelé aussi “l’argument Dominateur” ou encore “le Dominateur”) appartient à l’histoire de la philosophie et de la logique. Épictète rapporte que [8, p. 15], de la contradiction aperçue entre les énoncés A, B et C de la liste plus bas, Diodore aurait conclut à la négation de C, c’est-à-dire:
ce qui n’est ni actuellement ni à l’avenir est impossible.
Il est cependant douteux que la contradiction entre ces trois prémisses soit prouvable sans prémisses additionnelles; pour parvenir à une preuve remarquable en raison de son élégance, Prior [3] en a formulé deux, qui sont les énoncés D et E:
- Toute proposition vraie concernant le passé est nécessaire
- L’impossible ne suit pas logiquement du possible
- Il y a un possible qui n’est pas actuellement vrai et ne le sera pas
- Qu’un événement soit le cas implique qu’il n’existe aucun instant qui le précède où il est vrai que cet événement ne sera jamais.
- Si un événement n’est le cas ni maintenant ni à l’avenir, alors il existe un instant qui précède cet avenir après lequel cet événement ne sera jamais le cas.
En suivant la version semi-formelle que Fitting a donnée de la preuve de Prior, on traduit les énoncés de A à E respectivement par
une règle d’inférence ad hoc:
\begin{prooftree} \AxiomC{$\mathbf{P}Q$}\RightLabel{$\scriptsize{\lnot \Diamond \lnot \mathbf{P}}$}\UnaryInfC{$\lnot \Diamond \lnot \mathbf{P}Q$} \end{prooftree}la règle de logique modale \(\Diamond E\) [9, p. 71], [5, p. 39]:
\begin{prooftree} \AxiomC{$\Diamond Q$} \AxiomC{$\scriptsize{1}$}\noLine \UnaryInfC{$[Q]$} \noLine \UnaryInfC{$\vdots$} \noLine \UnaryInfC{$R$} \RightLabel{$\scriptsize{\Diamond ~ E ~1}$} \BinaryInfC{$\Diamond R$} \end{prooftree}ces trois formules:
\begin{equation} \label{eq:1} \Diamond Q \end{equation} \begin{equation} \label{eq:2} \lnot Q \end{equation} \begin{equation} \label{eq:3}\mathbf{\lnot F}Q \end{equation}un théorème de la logique temporelle minimale \(\mathbf{K_{t}}\) que l’on exprime sous forme inférentielle:
\begin{prooftree}\AxiomC{$Q$}\RightLabel{$\scriptsize{\mathbf{K_{t}}}$}\UnaryInfC{$\mathbf{\lnot P \lnot F}Q$} \end{prooftree}la formule suivante:
\begin{equation} \label{eq:4} (\lnot Q \land \mathbf{\lnot F}Q) \to \mathbf{P\lnot F}Q \end{equation}
En raison de la contradiction déduite de l’hypothèse \eqref{eq:1} et des prémisses \eqref{eq:2}, \eqref{eq:3} et \eqref{eq:4}, on rejette l’hypothèse \eqref{eq:1} en la niant, ce qui est exprimé par le séquent suivant:
\begin{equation} \label{eq:5} (\lnot Q \land \mathbf{\lnot F} Q) \to \mathbf{P \lnot F} Q, \lnot Q, \mathbf{\lnot F}Q \vdash \lnot \Diamond Q \end{equation}
3. Premier résultat: Prior remplace Diodore
On peut, en raison des règles de \(\mathbf{K_{t}}\) et de \(\mathbf{K}\), en conservant pour seules prémisses l’énoncé E de Prior et l’affirmation d’un événement quelconque qui ne sera jamais le cas, prouver une thèse plus simple que celle de Diodore: ce qui ne sera jamais est impossible.
Il suffit de simplifier \eqref{eq:4} par:
\begin{equation} \label{eq:6} \mathbf{\lnot F}Q \to \mathbf{P\lnot F}Q \end{equation}pour que le séquent suivant
\begin{equation} \label{eq:7} \mathbf{\lnot F} Q \to \mathbf{P \lnot F} Q, \mathbf{\lnot F}Q \vdash \lnot \Diamond Q \end{equation}soit prouvable:
\begin{prooftree} \AxiomC{$\scriptsize{1}$} \noLine \UnaryInfC{$Q$} \RightLabel{$\scriptsize{~\mathbf{K_{t}}}$} \UnaryInfC{$\mathbf{\lnot P \lnot F} Q$} \AxiomC{$\mathbf{\lnot F} Q \to \mathbf{P \lnot F}Q$} \AxiomC{$\mathbf{\lnot F}Q$} \RightLabel{$\scriptsize{~\to E}$} \BinaryInfC{$\mathbf{P \lnot F}Q$} \RightLabel{$\scriptsize{~\lnot E}$} \BinaryInfC{$\bot$} \RightLabel{$\scriptsize{~\lnot I~1}$} \UnaryInfC{$\lnot Q$} \RightLabel{$\scriptsize{~\Box I}$} \UnaryInfC{$\Box \lnot Q$} \RightLabel{$\scriptsize{\equiv}$} \UnaryInfC{$\lnot \Diamond Q$} \end{prooftree}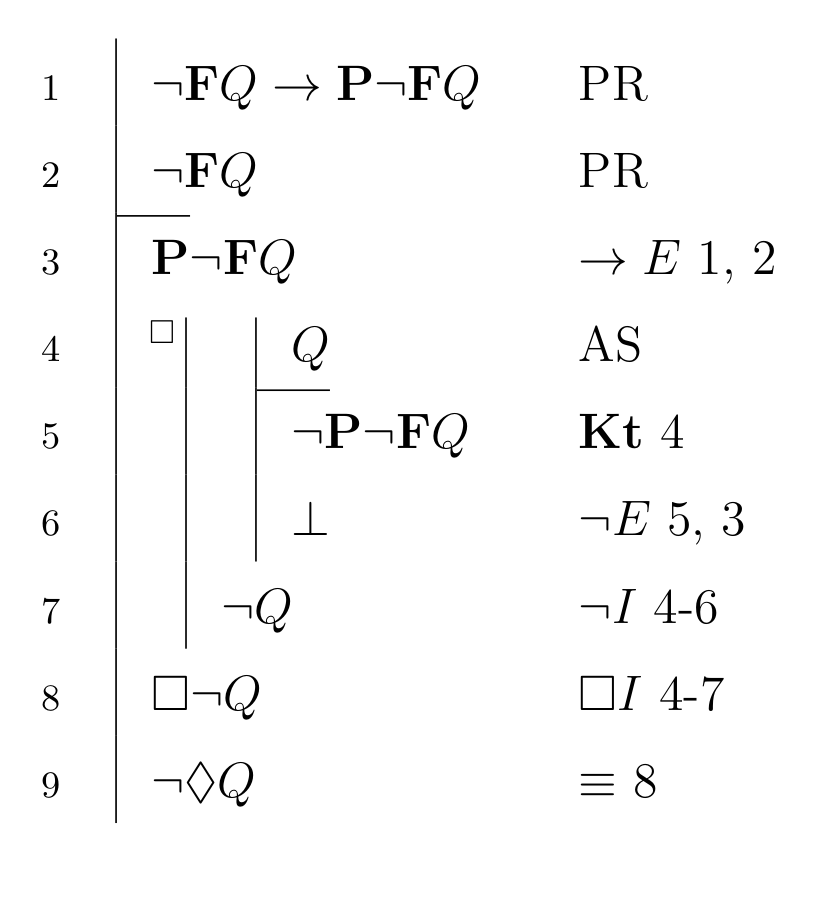
En raison des règles de \(\mathbf{K_{t}}\) et de \(\mathbf{K}\), le séquent \eqref{eq:5} est prouvable en se fondant uniquement sur les prémisses additionnelles de Fitting, c’est-à-dire sur les énoncés D et E.
À partir de la preuve du théorème précédent, la preuve est triviale.
4. Second résultat: l’argument DPF est valide dans le continu
Prior a fini par douter du caractère universellement valide de sa preuve de l’argument de Diodore. Ses doutes l’ont conduit à conclure que sa seconde prémisse additionnelle exprimée par \eqref{eq:4} n’est valide qu’à la condition d’imposer à la ligne du temps une structure discrète, c’est-à-dire une expression des instants fondée uniquement sur les nombres entiers (ou les entiers relatifs) et leur ordre [4, p. 49]. Dès lors que cette conclusion de Prior a été généralement acceptée [8, pp. 21–26], [5, p. 39] l’intérêt philosophique et historique de sa preuve est apparu comme limité. En effet, l’argument de Diodore était un argument polémique contre la conception aristotélicienne des modalités, or Aristote niait le caractère discret du temps; par conséquent, affirmer une prémisse explicitement rejetée par Aristote pour traduire le Dominateur n’est qu’un “aveu conscient d’impuissance”, comme l’a écrit Vuillemin [8, p. 24]. Le jugement est sévère, mais juste: un argument polémique qui s’appuie sur une thèse explicitement rejetée par l’adversaire perd évidemment toute pertinence.
Mais est-il absolument certain que la validité de \eqref{eq:4} exige que le temps ait une structure discrète? Remarquons que ce que soutient Prior et tous ceux qui l’ont suivi sur ce sujet est à la fois plus précis et plus complexe: \eqref{eq:4} exige une structure temporelle linéaire et discrète pour être valide et donc pour produire un authentique paradoxe, celui de Diodore, et même si à cette condition, l’argument de Diodore manque sa cible. Pour que ce qui suit soit totalement clair, il est utile de reprendre la partie de la preuve qui permet de déduire la prémisse majeure de l’argument DPF, et de l’écrire en raisonnant sur l’instant n de la façon suivante:
\begin{prooftree} \AxiomC{$n: (\lnot Q \land \mathbf{\lnot F} Q) \to \mathbf{P \lnot F}Q $} \AxiomC{$n: \lnot Q$} \AxiomC{$n: \mathbf{\lnot F}Q$} \RightLabel{$~\scriptsize{\land I}$} \BinaryInfC{$n: \lnot Q \land \mathbf{\lnot F}Q$} \RightLabel{$~\scriptsize{\to E}$} \BinaryInfC{$n: \mathbf{P\lnot F}Q $} \end{prooftree}Le schéma de déduction ci-dessus correspondant exactement à l’explication que Fitting et Mendelsohn donnent de \eqref{eq:4} [5, p. 39]:
If no sea battle is taking place and none will, then - and right here is where the assumption of the discreteness of time comes in - there was a time (for example, the moment just before the present) after which no sea battle would take place.
Supposons une ligne temporelle qui ne soit pas discrète, mais dense. Puisqu’en raison de cette hypothèse, il serait toujours possible de falsifier \eqref{eq:4}, en affirmant l’antécédent de ce conditionnel, c’est-à-dire \(n: \lnot C \land \mathbf{\lnot F}Q\), mais en falsifiant son conséquent, c’est-à-dire \(n: \mathbf{P \lnot F}Q\), car, pour le dire simplement, si proche soit-on de l’instant n, si la ligne du temps est dense, il y a toujours avant n une infinité d’instants où Q peut être le cas, si bien qu’avec l’hypothèse de la densité du temps, il existe une infinité de contre-modèles de \eqref{eq:4}. Or si \eqref{eq:4} n’est pas valide, alors le paradoxe disparaît; donc il faut admettre qu’admettre \eqref{eq:4}, c’est admettre que la ligne du temps doit être discrète, c’est-à-dire exprimée par exemple par l’ordre naturel des nombres entiers ou celui des entiers relatifs, et non dense comme ce serait le cas si l’on exprimait l’ordre temporel à l’aide de l’ordre de l’ensemble des nombres rationnels.
Notons que l’analyse de \eqref{eq:4} conduit à des paradoxes comparables à ceux de Zénon. Dans une structure dense, on se rapproche à l’infini de l’instant n à partir duquel Q n’est pas et ne sera jamais le cas, et donc tout se passe comme si on admettait la vérité d’un futur qui ne commencera jamais, puisqu’il y a toujours entre l’instant passé et l’instant à venir une infinité d’instants: le passé n’a pas de dernier instant et le futur n’en a pas de premier. Dans une structure discrète, comme le note pertinemment Russell [10], la temporalité se déroule par sauts d’instant en instant, et il ne semble pas moins absurde d’admettre qu’il n’y a aucune durée entre chaque instant, or c’est ce qu’implique cette représentation “cinématographique” du temps pour reprendre la célèbre expression de Bergson, dans des pages où il est également question des paradoxes de Zénon [11, pp. 753–757].
Notons maintenant que Fitting et Mendelsohn lisent \(\mathbf{P \lnot F}Q\) comme une expression désignant exclusivement un instant qui précède ce maintenant où ne se déroule aucune bataille navale, pour reprendre leur exemple. Mais ils négligent le fait que ce maintenant est envisagé depuis le futur, où aucune bataille navale ne se produira et donc commettent l’erreur qui consiste à exclure du passé un instant qui nécessairement lui appartient, quand on se place du point de vue de l’avenir, comme le confirme la formalisation dans le système de Volpe du raisonnement qui permet d’affirmer qu’il existe un instant passé après lequel il n’y aura aucune bataille navale:
\begin{prooftree} \AxiomC{$n: \lnot Q$} \AxiomC{$n: \mathbf{\lnot F}Q$} \RightLabel{$~\scriptsize{\land E}$} \BinaryInfC{$n: \mathbf{\lnot F}Q$} \AxiomC{$n < t$} \RightLabel{$\scriptsize{~\mathbf{P}I}$} \BinaryInfC{$t: \mathbf{P \lnot F}Q$} \end{prooftree}Cette règle exprime clairement ce que l’on appelle “la rétrogradation du vrai”: s’il est vrai en n que Q n’est pas et ne sera jamais le cas, cela signifie qu’en n’importe quel instant indiqué par t ultérieur à n, l’énoncé Q est faux; par conséquent, on pourra dire en t qu’il était vrai en n, que Q ne serait jamais le cas. À l’évidence, la règle \(\mathbf{P}I\) contient une notation à double indice temporel, où l’indice n est considéré, depuis l’indice t qui lui est postérieur, comme instant passé. Puisque c’est n qui, envisagé depuis le futur est naturellement considéré comme passé, alors, pour plus de précision et de clarté dans son expression, il serait possible d’alourdir la notation pour écrire la déduction qui précède de la façon suivante, où l’opérateur \(\mathbf{P}\) et n désignent le même point dans la ligne du temps:
\begin{prooftree} \AxiomC{$n: \lnot Q$} \AxiomC{$n: \mathbf{\lnot F}Q$} \RightLabel{$~\scriptsize{\land E}$} \BinaryInfC{$n: \mathbf{\lnot F}Q$} \AxiomC{$n < t$} \RightLabel{$\scriptsize{~\mathbf{P}I}$} \BinaryInfC{$t: \mathbf{\underset{\mathit{n}}P \lnot F}Q$} \end{prooftree}On transpose cette écriture à la déduction qui permet d’obtenir la prémisse majeure pour la déduction de la contradiction dans l’argument DPF:
\begin{prooftree} \AxiomC{$n: (\lnot Q \land \mathbf{\lnot F} Q) \to \mathbf{P \lnot F}Q $} \AxiomC{$n: \lnot Q$} \AxiomC{$n: \mathbf{\lnot F}Q$} \RightLabel{$~\scriptsize{\land I}$} \BinaryInfC{$n: \lnot Q \land \mathbf{\lnot F}Q$} \RightLabel{$~\scriptsize{\to E}$} \BinaryInfC{$n: \mathbf{\underset{\mathit{n}}P\lnot F}Q $} \end{prooftree}La conclusion de cette déduction peut alors se lire: “en n existe un instant qui est le passé de ce futur où Q ne sera jamais le cas”, en accord avec la signification de \(\mathbf{P \lnot F}Q\), l’indice n faisant alors référence à lui-même comme indice d’un instant qui est dans le passé du futur dont on parle, ce qui équivaut à relâcher la règle \(\mathbf{P}I\) en écrivant:
\begin{prooftree}\AxiomC{$a: Q$}\AxiomC{$a \leqslant b$}\RightLabel{$\scriptsize{~\mathbf{P}~I}$} \BinaryInfC{$b: \mathbf{P}Q$} \end{prooftree}pour ne pas alourdir le symbolisme.
Cette modification faite, il est alors facile de voir qu’il est faux que \eqref{eq:4} et \eqref{eq:6} exigent une structure discrète du temps pour être valides, car il suffit de faire de l’instant n où Q est déclaré comme toujours faux à l’avenir, la borne inférieure de l’avenir qui n’appartient pas à ce dernier [12, pp. 83–84], pour que \eqref{eq:6} et \eqref{eq:4} soient évidemment valides dans une structure temporelle linéaire et continue, en conformité avec un résultat de Bull [13] repris par Rescher et Urquhart [14, pp. 96–97]. On définit un modèle \(\mathcal{M}\) composé de deux périodes de temps consécutives \(S_{1}\) et \(S_{2}\), où n à la fois le dernier élément de \(S_{1}\) et la borne inférieure de la période \(S_{2}\) dénuée de premier instant. \(\mathcal{M}\) correspond à l’une des descriptions possibles d’un flux temporel continu [14, p. 96], où n joue le rôle de coupure de Dedekind entre \(S_{1}\) et \(S_{2}\). On conclut cette section par la preuve de la proposition suivante.
Dans un temps linéaire et continu où Q est déclaré en n comme toujours faux à l’avenir, il suffit de définir n comme la borne inférieure de cet avenir pour conclure que Q est impossible en n.
Dans le système de déduction naturelle étiquetée de Volpe, où l’on substitue \(\mathbf{\lnot P \lnot}\) à \(\mathbf{H}\) pour l’application de la règle \(\mathbf{H}I\), il suffit de raisonner sur la borne n pour obtenir le résultat recherché:
\begin{prooftree} \AxiomC{$~\scriptsize{1}$} \noLine \UnaryInfC{$[n: Q]$} \AxiomC{$~\scriptsize{2}$} \noLine \UnaryInfC{$[m < n]$} \RightLabel{$~\scriptsize{\mathbf{F}~ I}$} \BinaryInfC{$m: \mathbf{F}Q$} \RightLabel{$~\scriptsize{\mathbf{H}~I~2}$} \UnaryInfC{$n: \mathbf{\lnot P \lnot F} Q$} \AxiomC{$n: \mathbf{\lnot F} Q \to \mathbf{P \lnot F}Q$} \AxiomC{$n: \mathbf{\lnot F}Q$} \RightLabel{$~\scriptsize{\to~ E}$} \BinaryInfC{$n: \mathbf{P \lnot F}Q$} \RightLabel{$~\scriptsize{\lnot E}$} \BinaryInfC{$n: \bot$} \RightLabel{$~\scriptsize{\lnot ~ I~ 1}$} \UnaryInfC{$n: \lnot Q$} \RightLabel{$~\scriptsize{\Box ~I}$} \UnaryInfC{$\Box ~ n: \lnot Q$} \RightLabel{$~\scriptsize{\equiv}$} \UnaryInfC{$\lnot \Diamond ~ n: Q$} \end{prooftree}




